TEOREMA DE SENO, COSENO y TANGENTE

Teorema o ley del seno, coseno y tangente

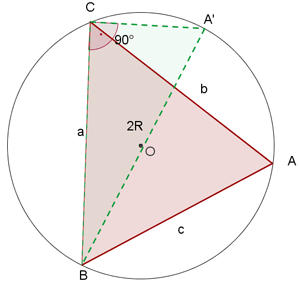
Teorema o ley del seno

Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.

Ejercicios

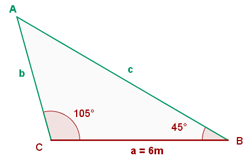
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Determina los restantes elementos.

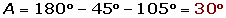
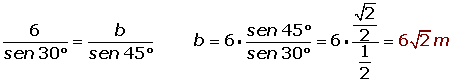
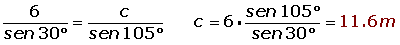
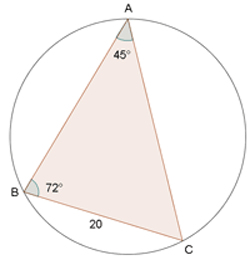
Hallar el radio del círculo circunscrito en un triángulo, donde A = 45°, B = 72° y a=20m.

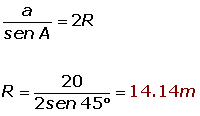
Teorema o ley del coseno

En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

Ejemplos

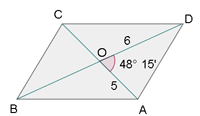
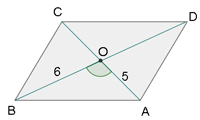
Las diagonales de un paralelogramo miden 10 cm y 12 cm, y el ángulo que forman es de 48° 15'. Calcular los lados.

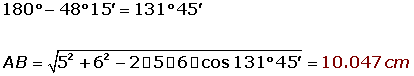
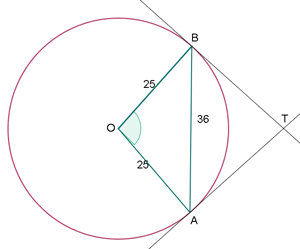
El radio de una circunferencia mide 25 m. Calcula el ángulo que formarán las tangentes a dicha circunferencia, trazadas por los extremos de una cuerda de longitud 36 m.

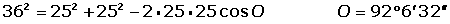
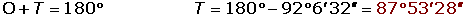
Teorema o ley de la tangente

Si A y B son ángulos de un triángulo y sus lados correspondientes son a y b, se cumple que:

Seno, coseno y tangente de 30º y 60º

Si dibujamos un triángulo equilátero ABC, cada uno de sus tres ángulos mide 60º y, si trazamos una altura del mismo, h, el ángulo del vértice A por el que la hemos trazado queda dividido en dos iguales de 30º cada uno. Recurriendo al Teorema de Pitágoras, tenemos que la altura es:

Seno, coseno y tangente de 45º

Razones trigonométricas de ángulos notables

Teorema del seno

En un triángulo cada lado es directamente proporcional al seno del ángulo opuesto.

Ejercicios

De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.

Calcular el radio del círculo circunscrito en un triángulo, donde A = 45°, B = 72° y a=20m.

Triángulos oblicuángulos

Para resolver triángulos oblicuángulos vamos a utilizar los teoremas del seno y del coseno.

Dependiendo de los elementos que conozcamos, nos encontramos con cuatro tipos de resolución de triángulos oblicuángulos:

1º. Conociendo un lado y dos ángulos adyacentes a él

De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.

2º. Conociendo dos lados y el ángulo comprendido

De un triángulo sabemos que: a = 10 m, b = 7 m y C = 30°. Calcula los restantes elementos.

3º Conociendo dos lados y un ángulo opuesto

sen B > 1. No hay solución

sen B = 1 Triángulo rectángulo

sen B < 1. Una o dos soluciones

Supongamos que tenemos a, b y A; al aplicar el teorema de los senos puede suceder:

1. sen B > 1. No hay solución.

Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 8 m.

Como el seno de un ángulo nunca puede ser mayor que 1, el problema no tiene solución. La figura muestra la imposibilidad de que exista el triángulo planteado.

2. sen B = 1. Solución única: triángulo rectángulo

Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 6 m.

3. sen B < 1. Una o dos soluciones

Resuelve el triángulo de datos: A = 60°, a = 8 m y b = 4 m.

Resuelve el triángulo de datos: A = 30°, a = 3 m y b = 4 m.

4º. Conociendo los tres lados

Resuelve el triángulo de datos: a = 15 m, b = 22 m y c = 17 m.

Teoremas de Trigonometría

Teorema de los senos

Cada lado de un triángulo es directamente proporcional al seno del ángulo opuesto.

Teorema del coseno

En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

Teorema de las tangentes