(Triángulo) - Teorema de Pitágoras (1801)

Triangulos semejantes y proporcionalidad

Ejercicios triángulos semejantes. 2/4. wmv

Círculo trigonométrico (PRIMERA PARTE)

Funciones Trigonométricas de Ángulos Notables: 30°, 60°, 45°, 37°, 53°

Valor de las razones trigonométricas en relacion a las del Primer Cuadrante

RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO

Solución de Triángulos Rectángulos - Solving right triangles

Solución de Triángulos Rectángulos - Solving right triangles

02.02 Tres ejercicios (Hallamos razones trigonométricas con la calculadora)

02.02 Tres ejercicios (Hallamos razones trigonométricas con la calculadora)
 

Teorema de Pitágoras

Para entrar en materia, es necesario recordar un par de ideas: Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º. En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos. 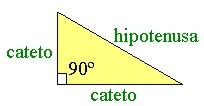Sabido esto, enunciemos el Teorema de Pitágoras: En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Recuerda: Este Teorema sólo se cumple para triángulos rectángulos. BC =  cateto   =  a CA =  cateto   =  b                          AB =  hipotenusa  =  c          La expresión matemática que representa este Teorema es: hipotenusa 2   =   cateto 2    +   cateto 2         c2    =     a2    +    b2 Si se deseara comprobar este Teorema se debe construir un cuadrado sobre cada cateto y sobre la hipotenusa y luego calcular sus áreas respectivas, puesto que el área del cuadrado construido sobre la hipotenusa de un triángulo es igual a la suma de las áreas de los cuadrados construidos sobre los catetos. El siguiente esquema representa lo dicho anteriormente: 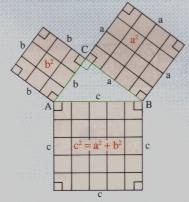                                         Una forma muy sencilla de explicar y de visualizar el Teorema de Pitágoras: En un triángulo rectángulo se verifica que el área del cuadrado construido sobre la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre los catetos. Es propiedad: www.profesorenlinea.cl. Registro Nº 188.540

02.01 Seis ejercicios (Conocida una razón trigonométrica, dibujar el ángulo)

02.01 Seis ejercicios (Conocida una razón trigonométrica, dibujar el ángulo)

TEMA: GUÍA N°2 ÁNGULO DE ELEVACIÓN Y ÁNGULO DE DEPRESIÓN

ACTIVIDAD N°1

Un árbol de 8cm de alto proyecta una sombra de 10cm de largo. Encontrar el ángulo de elevación del sol en ese momento.

ACTIVIDAD N°2

Un helicóptero está volando a 900m de altura, distingue un pueblo con un ángulo de depresión de 12°. ¿A qué distancia del pueblo se encuentra?

ACTIVIDAD N°3

Si miro hacia delante, observo u árbol cuya parte más alta tiene n ángulo de elevación de 40°, y se encuentra a 3.5m de distancia de mí. Si miro hacia atrás, observo un poste cuya parte más alta tiene un ángulo de elevación de 60°, y se encuentra a 2.5m de distancia de mí. Determina la altura de ambos objetos. (Depreciar la altura del sujeto)

ACTIVIDAD N°4

El ángulo de elevación del tope de un edificio es de 50° desde un punto A. Desde ese mismo punto, el ángulo de elevación hasta el tope de una antena sobre el edificio es de 60°. Sí la distancia desde el punto A hasta el tope de la antena es de 20m.

a) ¿Cuánto mide la antena?    ____________________

b) ¿Cuánto mide el edificio?  ____________________

ACTIVIDAD N°5

Desde lo alto de un faro, cuya altura sobre el nivel del mar es de 80 metros, el ángulo de depresión de una embarcación es de 15°. ¿A qué distancia del faro está la embarcación?

ACTIVIDAD N°6

Encontrar la altura de un árbol si el ángulo de elevación de un observador al extremo superior del mismo es 32°. La distancia del observador a la cúspide es de 19 metros.