Probabilidad y Estadística. Introducción a la distribución Binomial. UNE...

APRENDIENDO LAS RAZONES TRIGONOMETRICAS

Cálcular distancias desconocidas

Ejemplo para medir la altura de un edificio desde el suelo

Problemas trigonometria calcular distancias

1.  Juán y Pedro ven desde las puertas de sus casa una torre, bajo ángulos de 45° y 60°. La distancia entre sus casas es de 126 m y la torre está situada entre sus casas. Halla la altura de la torre.

Hacemos un dibujo con los datos.

Al trazar la altura de la torre se origina dos triángulos rectángulos.

Si llamamos x a la distancia de uno de los observadores al pie de la torre, la distancia del otro debe ser 126 - x.

Utilizamos las tangentes en ambos triángulos rectángulos, ya que tienen en conún un cateto que es la altura de la torre.

Planteamos el sistema de ecuaciones y resolvemos.

Ejercicios y problemas de trigonometria con soluciones

Actividades interactivas

>   Resolver cualquier triángulo, escribiendo los datos de los ángulos y lados que sepamos.

Resolución de Problemas

                       

En esta página se muestran ejemplos de ejercicios y problemas resueltos, relacionados con los contenidos de la unidad. En mayor o menor medida se abordan todos los tipos de ejercicios y problemas que se pueden hacer.
Nota: Todas las operaciones están redondeadas con dos o tres decimales.

EJERCICIO 1: Calcula las razones trigonométricas del ángulo α :

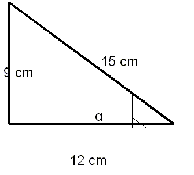
 Como ves, los tres lados del triángulo son conocidos, así que para calcular las razones trigonométricas sólo tenemos que aplicar las fórmulas y sustituir. Para el ángulo α el cateo opuesto es 9, el contiguo 12 y la hipotenusa 15.

                                 

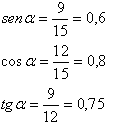
EJERCICIO 2: Calcula las razones trigonométricas del ángulo C del siguiente triángulo

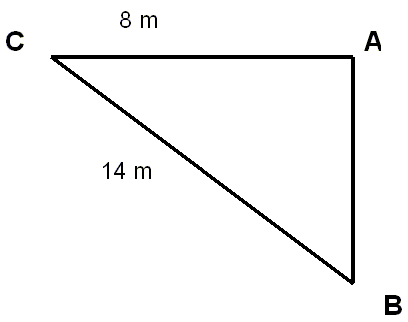
 Ahora en este ejercicio ya no tenemos los tres lados, falta uno de los catetos y para calcularlo vamos a utilizar el Teorema de Pitágoras.

Lo primero ponerle nombre a los lados. Vamos a llamarle con letras minúsculas a los lados que están enfrente del ángulo con la correspondiente letra mayúscula;    es decir a = 14 m, b = 8 m y c es el lado que queremos calcular

Aplicando el Teorema de Pitágoras tenemos:

                   a² = b² + c ²
                  14²= 8² + c²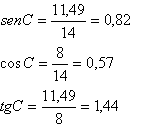 
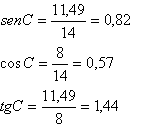
                 196 = 64 + c²
           196 - 64 = c²
                  132 = c²                        y aplicando las fórmulas
               11,49 = c                                    tenemos:

          Luego c = 11, 49 m. 

EJERCICIO 3: Determina los ángulos del ejercicio anterior

Obviamente ya sabemos que el ángulo A es el ángulo recto y por tanto A = 90º. Para calcular los otros dos vamos a hacerlo con las razones trigonométricas y con la ayuda de la calculadora.

Si queremos calcular el ángulo C con los datos que parto, lo primero es identificar los lados que conozco respecto al ángulo C, que en este caso son cateto contiguo e hipotenusa y pienso en qué razón trigonométrica intervienen esos lados. La respuesta es el coseno, así que calculo cos C

Cos C = 8 / 14 = 0,57. Ahora con la calculadora sacamos cuál es el ángulo, utilizando la función inversa de la tecla "cos", y el resultado es C = 55,25º.

Para calcular B puedo hacer lo mismo, pensar qué razón puedo calcular, o como ya tengo dos ángulos, sacarlo de que la suma de los ángulos de cualquier triángulo es 180º ( A + B + C = 180). Por cualquier camino el resultado es B = 34,75º.

EJERCICIO 4: De un triángulo rectángulo se sabe que uno de sus ángulo agudos es 40º y que el cateto opuesto a éste mide 10m. Calcula el ángulo y los lados que faltan.

Lo primero es hacer un dibujo que nos aclare la situación y ponerle nombre a los lados y ángulos

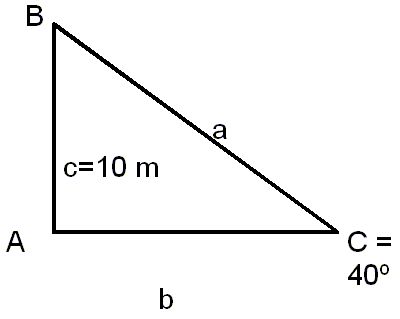
 Esta sería nuestra situación.

Para empezar los más fácil es sacar el ángulo que falta, y aplicando que la suma de los tres es 180, el ángulo B vale 50º.

Vamos a calcular ahora por ejemplo el lado "b". Si me fijo en el ángulo C, el lado que sé es el cateto opuesto y el que pretendo calcular es el contiguo. Como la razón trigonométrica en la que intervienen estos es la tangente, voy a calcularla con la calculadora y despejar a partir de ahí:

                   

Por tanto ya tenemos el lado "b". Para calcular el lado "a" podríamos aplicar Pitágoras o sacarlo por alguna razón. Vamos a seguir este camino que será más corto.
Por ejemplo voy a fijarme en el lado "c" y el ángulo "C", aunque ya podría utilizar cualquiera de los datos que tengo. Para el ángulo "C" sé cateto opuesto y quiero hipotenusa; así que habrá que utilizar el seno:

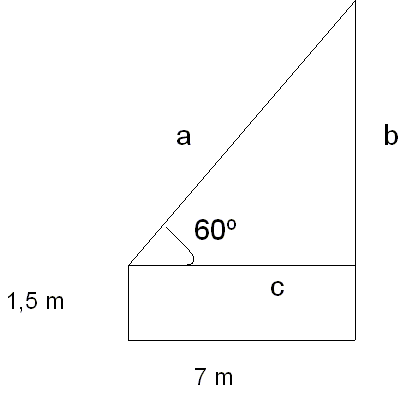
EJERCICIO 5: Calcula la altura de la torre si nuestro personaje está a 7 m de la base de la torre, el ángulo con el que está observando la cúspide es de 60º y sostiene el artilugio a una altura de 1,5 m.

 Para comenzar, vamos a hacer un dibujo que aclare un poco la situación poniendo los datos que conocemos.

Si nos fijamos en el triángulo, el lado c mide 7 m y una vez que tengamos calculado el lado b, para calcular la altura de la torre sólo tendremos que sumarle los 1,5 m. Así pues, vamos a calcular el lado b.

Para el ángulo 60º, el lado que conozco es el cateto contiguo y el que quiero calcular es el cateto opuesto, así pues planteo la tangente de 60º.

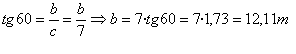
Por tanto la altura de la torre es 12,11 m + 1,5 m = 13, 61 m.

EJERCICIO 6: El seno de cierto ángulo α del segundo cuadrante vale 0,45. Calcula el coseno y la tangente.

Para resolver este ejercicio tenemos que recurrir a las relaciones trigonométricas. De la primera sacaremos el valor del coseno y una vez que lo tengamos sacaremos la tangente:

Sacamos el valor del coseno despejándolo de la fórmula:     sen²α  + cos²α  = 1.

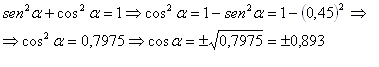
Como nuestro ángulo está en el segundo cuadrante y en ese cuadrante el coseno es negativo, tenemos que quedarnos con el signo -, por tanto cos α = - 0,893.

Para calcular el valor de la tangente, aplicamos la segunda fórmula:  

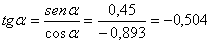
EJERCICIO 7: Sabiendo que cos 42º = 0,74. Calcula:
sen 222º,  tg 138º,  cos 48º,  sen 318º y    sen 132º.

sen 222º

El ángulo 222º pertenece al tercer cuadrante. Vamos a ver con que ángulo del primero se relaciona: α = 222º - 180º = 42º.
Por tanto y teniendo en cuenta que el seno en el tercer cuadrante es negativo, sen222º = - sen 42º = - 0,669 (Para calcular el sen 42º seguimos el mismo procedimiento que en el ejercicio 6).

tg 138º

138º está en el segundo cuadrante y se relaciona del primero con α = 180º - 138º = 42º, que vuelve a ser el ángulo que conocemos.
Como la tangente es negativa en el segundo cuadrante, tg 138º= - tg 42º= -0,9 (tg 42º lo calculamos igual que en el ejercicio 6)

cos 48º

48º es del primer cuadrante, pero cumple que es el complementario del ángulo que conozco 42º.
Entonces cos 48º = sen 42º = 0,669.

sen 318º

318º está en el cuarto cuadrante y se relaciona con 360º - 318º = 42.
Entonces sen 318 º= - sen 42º = - 0,669

sen132º

132º es del segundo y se relaciona con 180º - 132º = 48º que es el complementario de 42º.
Entonces y como el seno es positivo en el segundo cuadrante, sen 132º = sen 48º = cos 42º = 0,74.

Ahora te toca ti. Pincha en el  menú en el apartado "Ejercicios" , accede a los ejercicios propuestos y comprueba lo que has aprendido.

APLICACIÓN DE LA TRIGONOMETRÍA Cálculo de la altura de una montaña 1

Problema de aplicación de razones trigonométricas

Problema de Trigonometría con Triángulos Rectángulos

Los libros de La Biblia

DISTRIBUCIÓN NORMAL

Variable aleatoria de la distribución normal

Una variable aleatoria continua, X, sigue una distribución normal de media μ y desviación típica σ, y se designa por N(μ, σ), si se cumplen las siguientes condiciones:

1. La variable puede tomar cualquier valor: (-∞, +∞)

2. La función de densidad, es la expresión en términos de ecuación matemática de la curva de Gauss:

Curva de la distribución normal

El campo de existencia es cualquier valor real, es decir, (-∞, +∞).

Es simétrica respecto a la media µ.

Tiene un máximo en la media µ.

Crece hasta la media µ y decrece a partir de ella.

En los puntos µ − σ y µ + σ presenta puntos de inflexión.

El eje de abscisas es una asíntota de la curva.

El área del recinto determinado por la función y el eje de abscisas es igual a la unidad.

Al ser simétrica respecto al eje que pasa por x = µ, deja un área igual a 0.5 a la izquierda y otra igual a 0.5 a la derecha.

La probabilidad equivale al área encerrada bajo la curva.

p(μ - σ < X ≤ μ + σ) = 0.6826 = 68.26 %

p(μ - 2σ < X ≤ μ + 2σ) = 0.954 = 95.4 %

p(μ - 3σ < X ≤ μ + 3σ) = 0.997 = 99.7 %

N(0, 1)

La distribución normal estándar, o tipificada o reducida, es aquella que tiene por media el valor cero, μ = 0, y por desviación típica la unidad, σ =1.

Su función de densidad es:

Su gráfica es:

La probabilidad de la variable X dependerá del área del recinto sombreado en la figura. Y para calcularla utilizaremos una tabla.

Tipificación de la variable

Para poder utilizar la tabla tenemos que transformar la variable X que sigue una distribución N(μ, σ) en otra variable Z que siga una distribución N(0, 1).

Tabla de la curva normal (0, 1)

La tabla nos da las probabilidades de P(z ≤ k), siendo z la variable tipificada.

Estas probabilidades nos dan la función de distribución Φ(k).

Φ(k) = P(z ≤ k)

Búsqueda en la tabla de valor de k

Unidades y décimas en la columna de la izquierda.

Céntesimas en la fila de arriba.

P(Z ≤ a)

P(Z ≤ 1.47) = 0.9292

P(Z > a) = 1 - P(Z ≤ a)

P(Z > 1.47) = 1 − P(Z ≤ 1.47) = 1 − 0.9292 = 0.0708

P(Z ≤ −a) = 1 − P(Z ≤ a)

P(Z ≤ −1.47) = 1 − P(Z ≤ 1.47) = 1 − 0.9292 = 0.0708

P(Z > −a) = P(Z ≤ a)

p(Z > 1.47) = p(Z ≤ 1.47) = 0.9292

P(a < Z ≤ b ) = P(Z ≤ b) − P(Z ≤ a)

P( 0.45 <Z ≤ 1.47) = P(Z ≤ 1.47) − P(Z ≤ 0.45) =

= 0.9292 − 0.6736 = 0.2556

P(−b < Z ≤ −a ) = P(a < Z ≤ b )

P(−1.47 <Z ≤ − 0.45) = P( 0.45 <Z ≤ 1.47) =

= P(Z ≤ 1.47) − P(Z ≤ 0.45) = 0.9292 − 0.6736 = 0.2556

P(−a < Z ≤ b ) = P(Z ≤ b) − [ 1 − P(Z ≤ a)]

P(-1.47 < Z ≤ 0.45) = P(Z ≤ 0.45) − [ 1 − P(Z ≤ 1.47)]=

= 0.6736 − (1 − 0.9292) = 0.6028

p = K

Nos encontramos con el caso inverso a los anteriores, conocemos el valor de la probabilidad y se trata de hallar el valor de la abscisa. Ahora tenemos que buscar en la tabla el valor que más se aproxime a K.

p = 0.75Z ≤ 0.68

Para calcular la variable X nos vamos a la fórmula de la tipificación.

(X - μ)/σ = 0.68X = μ + 0.68 σ

Aproximación de la binomial por la normal

Teorema de Moivre

Si:

n·p ≥ 0 y n·q ≥ 0.

La distribución binomial B(n, p) se puede aproximar mediante una distribución normal:

Ejemplo

En una ciudad una de cada tres familias posee teléfono. Si se eligen al azar 90 familias, calcular la probabilidad de que entre ellas haya por lo menos 30 tengan teléfono.

PROBABILIDADES

PROBABILIDADES

Definición de probabiidad

La probabilidad de un suceso es un número, comprendido entre 0 y 1, que indica las posibilidades que tiene de verificarse cuando se realiza un experimento aleatorio.

Experimentos deterministas

Son los experimentos de los que podemos predecir el resultado antes de que se realicen.

Ejemplo

Si dejamos caer una piedra desde una ventana sabemos, sin lugar a dudas, que la piedra bajará. Si la arrojamos hacia arriba, sabemos que subirá durante un determinado intervalo de tiempo; pero después bajará.

Experimentos aleatorios

Son aquellos en los que no se puede predecir el resultado, ya que éste depende del azar.

Ejemplos

Si lanzamos una moneda no sabemos de antemano si saldrá cara o cruz.

Si lanzamos un dado tampoco podemos determinar el resultado que vamos a obtener.

Teoría de probabilidades

La teoría de probabilidades se ocupa de asignar un cierto número a cada posible resultado que pueda ocurrir en un experimento aleatorio, con el fin de cuantificar dichos resultados y saber si un suceso es más probable que otro. Con este fin, introduciremos algunas definiciones:

Suceso

Es cada uno de los resultados posibles de una experiencia aleatoria.

Al lanzar una moneda salga cara.

Al lanzar una moneda se obtenga 4.

Espacio muestral

Es el conjunto de todos los posibles resultados de una experiencia aleatoria, lo representaremos por E (o bien por la letra griega Ω).

Espacio muestral de una moneda:

E = {C, X}.

Espacio muestral de un dado:

E = {1, 2, 3, 4, 5, 6}.

Suceso aleatorio

Suceso aleatorio es cualquier subconjunto del espacio muestral.

Por ejemplo al tirar un dado un suceso sería que saliera par, otro, obtener múltiplo de 3, y otro, sacar 5.

Ejemplo

Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas. Calcular:

1. El espacio muestral.

E = {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b); (n, n,n)}

2. El suceso A = {extraer tres bolas del mismo color}.

A = {(b,b,b); (n, n,n)}

3. El suceso B = {extraer al menos una bola blanca}.

B= {(b,b,b); (b,b,n); (b,n,b); (n,b,b); (b,n,n); (n,b,n); (n,n ,b)}

4. El suceso C = {extraer una sola bola negra}.

C = {(b,b,n); (b,n,b); (n,b,b)}

Suceso elemental

Suceso elemental es cada uno de los elementos que forman parte del espacio muestral.

Por ejemplo al tirar un dado un suceso elemental es sacar 5.

Suceso compuesto

Suceso compuesto es cualquier subconjunto del espacio muestral.

Por ejemplo al tirar un dado un suceso sería que saliera par, otro, obtener múltiplo de 3.

Suceso seguro

Suceso seguro, E, está formado por todos los posibles resultados (es decir, por el espacio muestral).

Por ejemplo al tirar un dado un dado obtener una puntuación que sea menor que 7.

Suceso imposible

Suceso imposible, , es el que no tiene ningún elemento.

Por ejemplo al tirar un dado obtener una puntuación igual a 7.

Sucesos compatibles

Dos sucesos, A y B, son compatibles cuando tienen algún suceso elemental común.

Si A es sacar puntuación par al tirar un dado y B es obtener múltiplo de 3, A y B son compatibles porque el 6 es un suceso elemental común.

Sucesos incompatibles

Dos sucesos, A y B, son incompatibles cuando no tienen ningún elemento en común.

Si A es sacar puntuación par al tirar un dado y B es obtener múltiplo de 5, A y B son incompatibles.

Sucesos independientes

Dos sucesos, A y B, son independientes cuando la probabilidad de que suceda A no se ve afectada porque haya sucedido o no B.

Al lazar dos dados los resultados son independientes.

Sucesos dependientes

Dos sucesos, A y B, son dependientes cuando la probabilidad de que suceda A se ve afectada porque haya sucedido o no B.

Extraer dos cartas de una baraja, sin reposición, son sucesos dependientes.

Suceso contrario

El suceso contrario a A es otro suceso que se realiza cuando no se realiza A. Se denota por .

Son sucesos contrarios sacar par e impar al lanzar un dado.

Espacio de sucesos, S, es el conjunto de todos los sucesos aleatorios.

Si tiramos una moneda el espacio se sucesos está formado por:

S= {, {C}, {X}, {C,X}}.

Observamos que el primer elemento es el suceso imposible y el último el suceso seguro.

Si E tiene un número finito de elementos, n, de elementos el número de sucesos de E es 2ⁿ .

Una moneda E= {C, X}.

Número de sucesos = 2² =4

Dos monedas E= {(C,C); (C,X); (X,C); (X,X)}.

Número de sucesos = 2⁴ =16

Un dado E = {1, 2, 3, 4, 5, 6}.

Número de sucesos = 2⁶ = 64

Si A ₁, A ₂ ,... , A _n son:

Sucesos incompatibles 2 a 2.

Y cuya unión es el espacio muestral (A ₁ A ₂ ... A _n = E).

Y B es otro suceso.

Resulta que:

p(B) = p(A₁) · p(B/A₁) + p(A₂) · p(B/A₂ ) + ... + p(A_n) · p(B/A_n )

Ejemplo

Se dispone de tres cajas con bombillas. La primera contiene 10 bombillas, de las cuales hay cuatro fundidas; en la segunda hay seis bombillas, estando una de ellas fundida, y la tercera caja hay tres bombillas fundidas de un total de ocho. ¿Cuál es la probabilidad de que al tomar una bombilla al azar de una cualquiera de las cajas, esté fundida?

Axiomas de la probabilidad

1.La probabilidad es positiva y menor o igual que 1.

0 ≤ p(A) ≤ 1

2. La probabilidad del suceso seguro es 1.

p(E) = 1

3.Si A y B son incompatibles, es decir A B = entonces:

p(A B) = p(A) + p(B)

Propiedades de la probabilidad

1 La suma de las probabilidades de un suceso y su contrario vale 1, por tanto la probabilidad del suceso contrario es:

2 Probabilidad del suceso imposible es cero.

3 La probabilidad de la unión de dos sucesos es la suma de sus probabilidades restándole la probabilidad de su intersección.

4 Si un suceso está incluido en otro, su probabilidad es menor o igual a la de éste.

5 Si A₁, A₂, ..., A_k son incompatibles dos a dos entonces:

6 Si el espacio muestral E es finito y un suceso es S = {x₁, x₂, ..., x_n} entonces:

Por ejemplo la probabilidad de sacar par, al tirar un dado, es:

P(par) = P(2) + P(4) + P(6)

Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad.

En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).

Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1.

Ejemplos

Una clase consta de seis niñas y 10 niños. Si se escoge un comité de tres al azar, hallar la probabilidad de:

1 Seleccionar tres niños.

2Seleccionar exactamente dos niños y una niña.

3Seleccionar exactamente dos niñas y un niño.

1 Seleccionar tres niñas.

Calcular la probabilidad de que al arrojar al aire tres monedas, salgan:

Tres caras.

Experimentos compuestos

Un experimento compuesto es aquel que consta de dos o más experimentos aleatorios simples.

Es decir, si tiramos un dado, o una moneda, son experimentos aleatorios simples, pero si realizamos el experimento de tirar un dado y posteriormente una moneda, estamos realizando un experimento compuesto.

En los experimentos compuestos es conveniente usar el llamado diagrama en árbol para hacerse una idea global de todos ellos.

La función de probabilidad de la distribución binomial, también denominada función de la distribución de Bernoulli, es:

n es el número de pruebas.

k es el número de éxitos.

p es la probabilidad de éxito.

q es la probabilidad de fracaso.

El número combinatorio

Ejemplo

La última novela de un autor ha tenido un gran éxito, hasta el punto de que el 80% de los lectores ya la han leido. Un grupo de 4 amigos son aficionados a la lectura:

1. ¿Cuál es la probabilidad de que el grupo hayan leido la novela 2 personas?

n = 4

p = 0.8

q = 0.2

B(4, 0.8)

2.¿Y cómo máximo 2?